Contents
- 1 Question 1
- 2 Question 2
- 3 Question 3
- 4 Question 4
- 5 Question 5
- 6 Question 6
- 7 Question 7
- 8 Question 8
- 9 Question 9
- 10 Question 10
- 11 Question 11
- 12 Question 12
- 13 Question 13
- 14 Question 14
- 15 Question 15
- 16 Question 16
- 17 Question 17
- 18 Question 18
- 19 Question 19
- 20 Question 20
- 21 Question 21
- 22 Question 22
- 23 Question 23
- 24 Question 24
- 25 Question 25
- 26 Question 26
- 27 Question 27
- 28 Question 28
- 29 Question 29
Question 1
The mean of 11 results is 30. If the mean of the first 6 results is 28 and that of last 6 results is 32, find the 6th result.
Sol :
Let the 6th number be x
Given that mean of 11 results = 30
∴ sum of 11 numbers = 11 × 30 = 330
Mean of the first 6 results = 28
Sum of first 6 numbers = 6 × 28 = 168
Mean of the last 6 results = 32
Sum of the last 6 results = 6 × 32 = 192
Therefore,
Sum of first 6 numbers + sum of last 6 numbers – 6th number = sum of 11 numbers
168 + 192 – x = 330
⇒ 360 – x = 330
⇒ x = 30
Question 2
The mean of 17 observations is 20. If the mean of the first 9 observation is 23 and that of last 9 observations is 18, find the 9th observation.
Sol :
Let the 9th observation be x
Given that mean of 17 observations = 20
∴ sum of 17 observations = 17 × 20 = 340
Mean of the first 9 observations= 23
Sum of first 9 observations = 9 × 23 = 207
Mean of the last 9 observations = 18
Sum of the last 9 observations = 9 × 18 = 162
Therefore,
Sum of first 9 observations + sum of last 9 observations – 9th observation = sum of 17 observations
207 + 162 – x = 340
⇒ 369 – x = 340
⇒ x = 29
Question 3
The mean weight of 21 students of a class is 52 kg. If the mean weight of the first 11 students of the class is 50 kg and that of the last 11 students is 54 kg, find the weight of the 11th student.
Sol :
Let the weight of 11th student be x
Given that mean weight of 21 students = 52kg
∴ sum of 21 students weight = 21 × 52 = 1092kg
Mean weight of the first 11 students = 50kg
Sum of first 11 students weight = 11 × 50 = 550kg
Mean weight of the last 11 students = 54kg
Sum of the last 11 students weight = 11 × 54 = 594kg
Therefore,
Sum of first 11 students weight + sum of last 11 students weight – weight of the 11th student = sum of 21 students weight
550+594 – x = 1092
⇒ 1144 – x = 1092
⇒ x = 52
Hence, weight of 11th student is 52kg
Question 4
The mean weight of 25 students of a class is 60 kg. If the mean weight of the first 13 students of the class is 57 kg and that of the last 13 students is 63 kg, find the weight of the 13th student.
Sol :
Let the weight of 13th student be x
Given that mean weight of 25 students = 60kg
∴ sum of 25 students weight = 25 × 60 = 1500kg
Mean weight of the first 13 students = 57kg
Sum of first 13 students weight = 13 × 57 = 741kg
Mean weight of the last 13 students = 63kg
Sum of the last 13 students weight = 13 × 63 = 819kg
Therefore,
Sum of first 13 students weight + sum of last 13 students weight – weight of the 13th student = sum of 25 students weight
741 + 819 – x = 1500
⇒ 1560 – x = 1500
⇒ x = 60
Hence, weight of 13th student is 60kg
Question 5
The mean of 23 observations is 34. If the mean of the first 12 observations is 32 and that of the last 12 observations is 38, find the 12th observation.
Sol :
Let the 12th observation be x
Given that mean of 23 observations = 34
∴ sum of 23 observations = 23 × 34 = 782
Mean of the first 12 observations = 32
Sum of first 12 observations = 12 × 32 = 384
Mean of the last 12 observations = 38
Sum of the last 12 observations = 12 × 38 = 456
Therefore,
Sum of first 12 observations + sum of last 12 observations – 12th observation = sum of 23 observations
384 + 456 – x = 782
⇒ 840 – x = 782
⇒ x = 58
Question 6
The mean of 11 numbers is 35. If the mean of first 6 numbers is 32 and that of last 6 numbers is 37, find the 6th number.
Sol :
Let the 6th number be x
Given that mean of 11 results = 35
∴ sum of 11 numbers = 11 × 35 = 385
Mean of the first 6 results = 32
Sum of first 6 numbers = 6 × 32 = 192
Mean of the last 6 results = 37
Sum of the last 6 results = 6 × 37 = 222
Therefore,
Sum of first 6 numbers + sum of last 6 numbers – 6th number = sum of 11 numbers
192 + 222 – x = 385
⇒ 414 – x = 385
⇒ x = 29
Question 7
The mean of 25 observations is 36. If the mean of the first 13 observations is 32 and that of the last 13 observations is 39, find the 13th observation.
Sol :
Let the 13th observation be x
Given that mean of 25 observations = 36
∴ sum of 25 observations = 25 × 36 = 900
Mean of the first 13 observations = 32
Sum of first 13 observations = 13 × 32 = 416
Mean of the last 13 observations = 39
Sum of the last 13 observations = 13 × 39 = 507
Therefore,
Sum of first 13 observations + sum of last 13 observations – 13th observation = sum of 25 observations
416 + 507 – x = 900
⇒ 923 – x = 900
⇒ x = 23
Question 8
If the mean of the following data is 25, find the value of k.
| x | 5 | 15 | 25 | 35 | 45 |
| f | 3 | k | 3 | 6 | 2 |
Sol :
| xi | fi | xifi |
| 5 | 5 | 15 |
| 15 | K | 15k |
| 25 | 3 | 75 |
| 35 | 6 | 210 |
| 45 | 2 | 90 |
| Total | Σfi=14+k | Σfixi=390+15k |
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 25=\frac{390+15 k}{14+k}$
⇒25(14+k) = 390+ 15k
⇒350 + 25k = 390 + 15k
⇒ 25k – 15k = 390 – 350
⇒ 10k = 40
⇒ k = 4
Question 9
Find the arithmetic mean of the following distribution:
| Marks obtained | 10 | 15 | 20 | 25 | 30 |
| No. of students | 2 | 4 | 6 | 8 | 10 |
Sol :
| Marks obtained(xi) | No. of student(fi) | xifi |
| 10 | 2 | 20 |
| 15 | 4 | 60 |
| 20 | 6 | 120 |
| 25 | 8 | 200 |
| 30 | 10 | 300 |
| Total | Σfi=30 | Σfixi=700 |
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{700}{30}=23.33$
Question 10
The mean of the following frequency distribution is 62.8. Find the missing frequency x:
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 | 100-120 |
| Frequency | 5 | 8 | x | 12 | 7 | 8 |
Sol :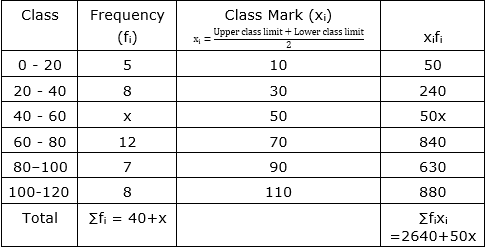
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 62.8=\frac{2640+50 \mathrm{x}}{40+\mathrm{x}}$
⇒62.8 (40 + x) = 2640 + 50x
⇒2512 + 62.8x = 2640 + 50x
⇒ 62.8x – 50x = 2640 – 2512
⇒ 12.8x = 128
⇒ x = 10
Question 11
The arithmetic mean of the following data is 14. Find the value of p:
| x | 5 | 10 | 15 | 20 | 25 |
| f | 7 | p | 8 | 4 | 5 |
Sol :
| (xi) | (fi) | xifi |
| 5 | 7 | 35 |
| 10 | p | 10p |
| 15 | 8 | 120 |
| 20 | 4 | 80 |
| 25 | 5 | 125 |
| Total | Σfi=24+p | Σfixi=360+10p |
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 14=\frac{360+10 p}{24+p}$
⇒14 (24+p) = 360 + 10p
⇒336 + 14p = 360 + 10p
⇒ 14p – 10p = 360 – 336
⇒ 4p = 24
⇒ p = 6
Question 12
If the mean of the following data is 18, find the missing frequency p:
Sol :
| (xi) | (fi) | xifi |
| 10 | 5 | 50 |
| 15 | 10 | 150 |
| 20 | p | 20p |
| 25 | 8 | 200 |
| Total | Σfi=23+p | Σfixi=400+20p |
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 18=\frac{400+20 p}{23+p}$
⇒18 (23 + p) = 400 + 20p
⇒414 + 18p = 400 + 20p
⇒ 18p – 20p = 400 – 414
⇒ -2p = -14
⇒ p = 7
Question 13
Find the value of p if the mean of the following distribution is 7.5:
| x | 3 | 5 | 7 | 9 | 11 | 13 |
| f | 6 | 8 | 15 | p | 8 | 4 |
Sol :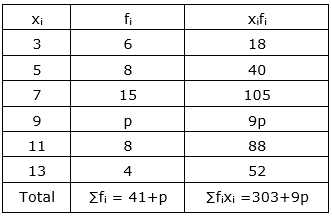
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 7.5=\frac{303+9 p}{41+p}$
⇒7.5(41+p) = 303 + 9p
⇒307.5 + 7.5p = 303 + 9p
⇒ 7.5p – 9p = 303 – 307.5
⇒ -1.5p = -4.5
⇒ p = 3
Question 14
Find the mean of the following data:
| Class interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 12 | 11 | 8 | 10 | 9 |
Sol :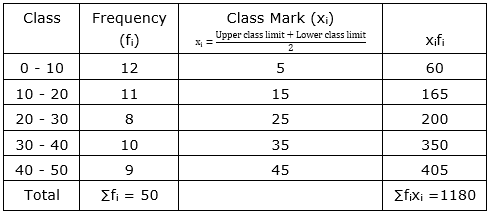
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}=\frac{1180}{50}=23.6$
Question 15
Find the mean of the following distribution:
Sol :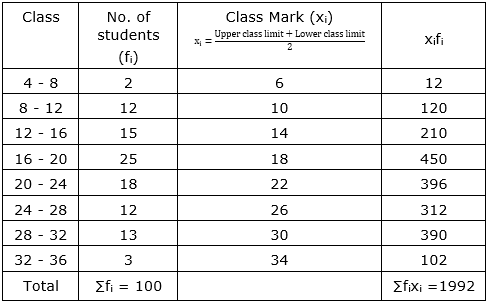
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}=\frac{1992}{100}=19.92$
Question 16
The arithmetic mean of the following frequency distribution is 53. Find the value of p:
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Frequency | 12 | 15 | 32 | p | 13 |
Sol :
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 53=\frac{1900+70 p}{72+p}$
⇒53 (72+p) = 3340 + 70p
⇒3816 + 53p = 3340 + 70p
⇒ 53p – 70p = 3340 – 3816
⇒ -17p = -476
⇒ p = 28
Question 17
If the mean of the following distribution is 5. Find the value of f1:
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Frequency | 17 | 28 | 32 | f1 | 19 |
Sol :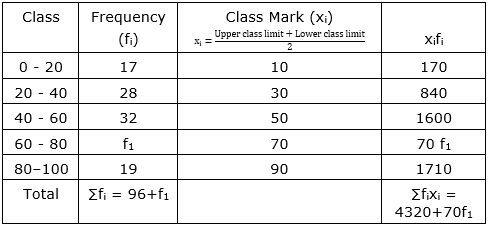
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 5=\frac{4320+70 f_{1}}{96+f_{1}}$
⇒ 5(96+ f1) = 4320 + 70f1
⇒480 + 5f1 = 4320 + 70f1
⇒ 5f1 – 70f1 = 4320 – 480
⇒ -65f1 = +3840
⇒ f1 = – 59.07
This is not possible as frequency can not be negative.
Question 18
Find the mean of the following frequency distribution:
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Frequency | 15 | 18 | 21 | 29 | 17 |
Sol :
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{5300}{100}=53$
Question 19
The mean of the following frequency distribution is 62.8 and the sum of all frequency is 50. Compute the missing frequency f1 and f2 :
| Class | 0-20 | 2040 | 40-60 | 60-80 | 80-100 | 100-120 | Total |
| Frequency | 5 | f1 | 10 | f2 | 7 | 8 | 50 |
Sol :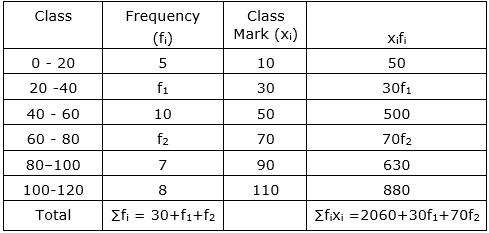
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 62.8=\frac{2060+30 f_{1}+70 f_{2}}{50}$ [given: ∑fi = 50]
⇒ 62.8(50) = 2060 + 30f1 +70f2
⇒ 3140 = 2060 + 30f1 +70f2
⇒ 3140 – 2060 = 30f1 +70f2
⇒ 1080 = 30f1 +70f2
⇒ 108 = 3f1 +7f2 …(i)
and 30 + f1 +f2 = 50
⇒ f1 +f2 = 50 – 30
⇒ f1 +f2 = 20
⇒ f1 = 20 – f2 …(ii)
Now, putting the value of f1 in eq. (i), we get
3(20 –f2) + 7f2 = 108
⇒ 60 – 3f2 + 7f2 = 108
⇒ 4f2 = 108 – 60
⇒ 4f2 = 48
⇒ f2 = 12
Now, substitute the value of f2 in eq. (ii), we get
f1 = 20 – 12
⇒ f1 = 8
Question 20
The mean of the following frequency distribution is 57.6 and the sum of the frequencies is 50. Find the missing frequencies f1 and f2 :
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 | 100-120 |
| Frequency | 7 | f1 | 12 | f2 | 8 | 5 |
Sol :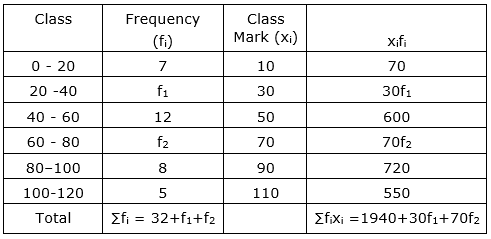
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{j}}}{\sum \mathrm{f}_{\mathrm{i}}}$
$\Rightarrow 57.6=\frac{2060+30 f_{1}+70 f_{2}}{50}$ [given: ∑fi = 50]
⇒ 57.6(50) = 1940 + 30f1 +70f2
⇒ 2880 = 1940 + 30f1 +70f2
⇒ 2880 – 1940 = 30f1 +70f2
⇒ 940 = 30f1 +70f2
⇒ 94 = 3f1 +7f2 …(i)
and 32 + f1 +f2 = 50
⇒ f1 +f2 = 50 – 32
⇒ f1 +f2 = 18
⇒ f1 = 18 – f2 …(ii)
Now, putting the value of f1 in eq. (i), we get
3(18 –f2) + 7f2 = 94
⇒ 54 – 3f2 + 7f2 = 94
⇒ 4f2 = 94 – 54
⇒ 4f2 = 40
⇒ f2 = 10
Now, substitute the value of f2 in eq. (ii), we get
f1 = 18 – 10
⇒ f1 = 8
Question 21
Find the mean of the following data:
| Class Interval | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| Frequency | 8 | 6 | 12 | 11 | 13 |
Sol :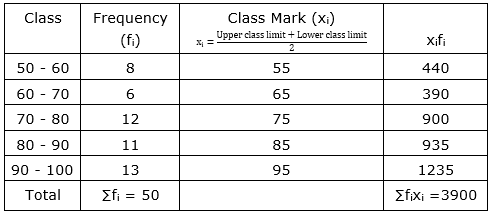
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}=\frac{3900}{50}=78$
Question 22
Find the mean of the following frequency distribution:
| Class Interval | 15-25 | 25-35 | 35-45 | 45-55 | 55-56 |
| Frequency | 60 | 35 | 22 | 18 | 15 |
Sol :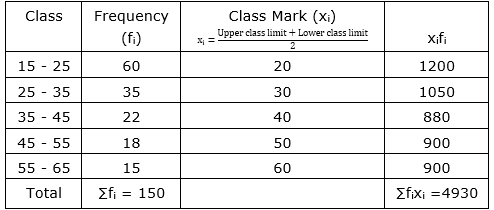
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}=\frac{4930}{150}=32.87$
Question 23
Find the mean of the following frequency distribution:
| Class | 50-60 | 70-90 | 90-110 | 110-130 | 130-150 | 150-170 |
| Frequency | 18 | 12 | 13 | 27 | 8 | 22 |
Sol :
Here, the class size varies, and xi’s are large. Now, we apply the step deviation method with a = 120 and h = 20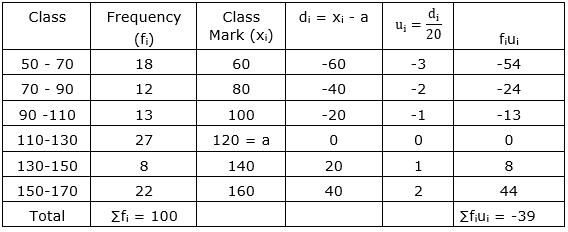
Now, $\overline{\mathrm{x}}=\mathrm{a}+\mathrm{h}\left(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\right)$
$\Rightarrow \overline{\mathrm{x}}=120+20\left(\frac{-39}{100}\right)$
$\Rightarrow \overline{\mathrm{x}}=120+\left(\frac{-78}{10}\right)$
$\Rightarrow \overline{\mathrm{x}}=\frac{1200-78}{10}$
⇒ $\overline{\mathrm{x}}$= 112.2
Question 24
Find the mean of the following frequency distribution:
| Class | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 |
| Frequency | 14 | 22 | 16 | 6 | 5 | 3 | 4 |
Sol :
Here, we can see that the class interval is not continuous. So, we make it continuous.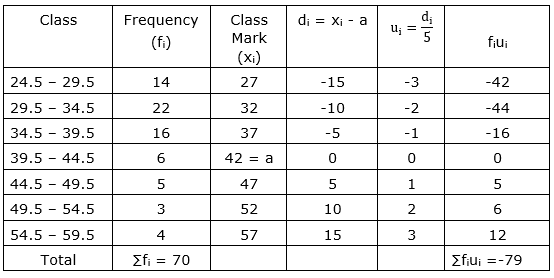
Now, $\overline{\mathrm{x}}=\mathrm{a}+\mathrm{h}\left(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\right)$
$\Rightarrow \overline{\mathrm{x}}=42+5\left(\frac{-79}{70}\right)$
$\Rightarrow \bar{x}=\frac{2940-395}{70}$
⇒ x̄ = 36.36
Question 25
The following table gives the marks scored by 50 students in a class-test:
| Marks | 0-100 | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 |
| No. of students | 2 | 8 | 12 | 20 | 5 | 3 |
Find the mean marks scored by a student in the class-test.
Sol :
Here, the xi’s are large. Now, we apply the step deviation method with a = 350 and h = 100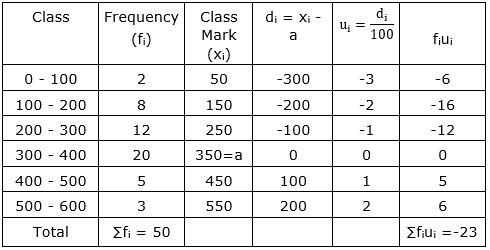
Now, $\overline{\mathrm{x}}=\mathrm{a}+\mathrm{h}\left(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\right)$
$\Rightarrow \bar{x}=350+100\left(\frac{-23}{50}\right)$
⇒x̄ = 350 – 46
⇒x̄ = 304
Hence, the mean marks scored by a student in the class-test is 304
Question 26
Find the mean of the following data:
| Class Interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 3 | 5 | 9 | 5 | 3 |
Sol :
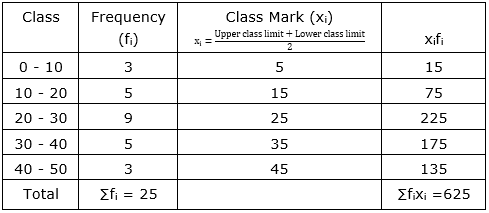
Now, $\overline{\mathrm{x}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}=\frac{625}{25}=25$
Question 27
Find the mean of the following data:
| Class Interval | 0-100 | 100-200 | 200-300 | 300-400 | 400-500 |
| Frequency | 6 | 9 | 15 | 12 | 8 |
Sol :
Here, the xi’s are large. Now, we apply the step deviation method with a = 250 and h = 100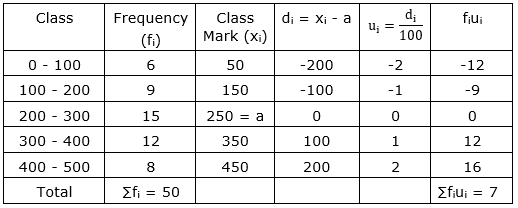
Now, $\overline{\mathrm{x}}=\mathrm{a}+\mathrm{h}\left(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\right)$
$\Rightarrow \overline{\mathrm{x}}=250+100\left(\frac{7}{50}\right)$
⇒x̄ = 250 + 14
⇒x̄ = 264
Question 28
The following table gives the marks scored by 80 students in a class-test:
| Marks | 0-50 | 50-100 | 100-150 | 150-200 | 200-250 | 250-300 |
| No. of students | 8 | 12 | 20 | 25 | 10 | 5 |
Find the mean marks scored by a student in the class-test.
Sol :
Here, the xi’s are large. Now, we apply the step deviation method with a = 175 and h = 50
Now, $\overline{\mathrm{x}}=\mathrm{a}+\mathrm{h}\left(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\right)$
$\Rightarrow \bar{x}=175+50\left(\frac{-48}{80}\right)$
⇒x̄ = 175 – 30
⇒x̄ = 145
Hence, the mean marks scored by a student in the class-test is 145
Question 29
The following table gives the distribution of expenditure of different families on education. Find the mean expenditure on education of a family:
| Expenditure (in Rs) | Number of Families |
| 1000-1500 | 24 |
| 1500-2000 | 40 |
| 2000-2500 | 33 |
| 2500-3000 | 28 |
| 3000-3500 | 30 |
| 3500-4000 | 22 |
| 4000-4500 | 16 |
| 4500-5000 | 7 |
Sol :
Here, the xi’s are large. Now, we apply the step deviation method with a = 3250 and h = 500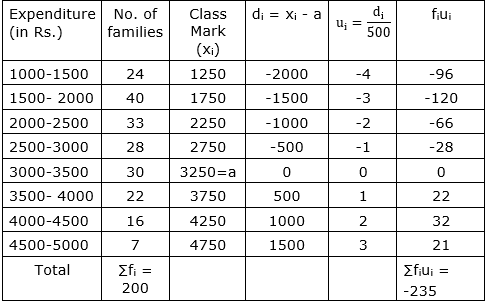
Now, $\overline{\mathrm{x}}=\mathrm{a}+\mathrm{h}\left(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\right)$
$\Rightarrow \bar{x}=3250+500\left(\frac{-235}{200}\right)$
⇒x̄ = 3250 – 587.5
⇒x̄ = 2662.5
Hence, the mean expenditure on education of a family is Rs 2662.5
