Contents
The syllabus for SAAT 2024 has been released by Siksha ‘O’ Anusandhan (deemed to be University) (SOA University). If you are gearing up for the Siksha ‘O’ Anusandhan Admission Test, you can access and download the SAAT Syllabus PDF to aid your exam preparation. The syllabus for the SAAT exam outlines the subjects and topics that need to be studied for the entrance test.
By thoroughly covering the exam syllabus and addressing other aspects of SAAT preparation, you can aspire to achieve a commendable score and rank in SAAT 2024.
SAAT Syllabus
SAAT 2024 Syllabus PDF Download Link – You can download the 2024 syllabus as per its issuance by SOA University at admission.soa.ac.in or here.



































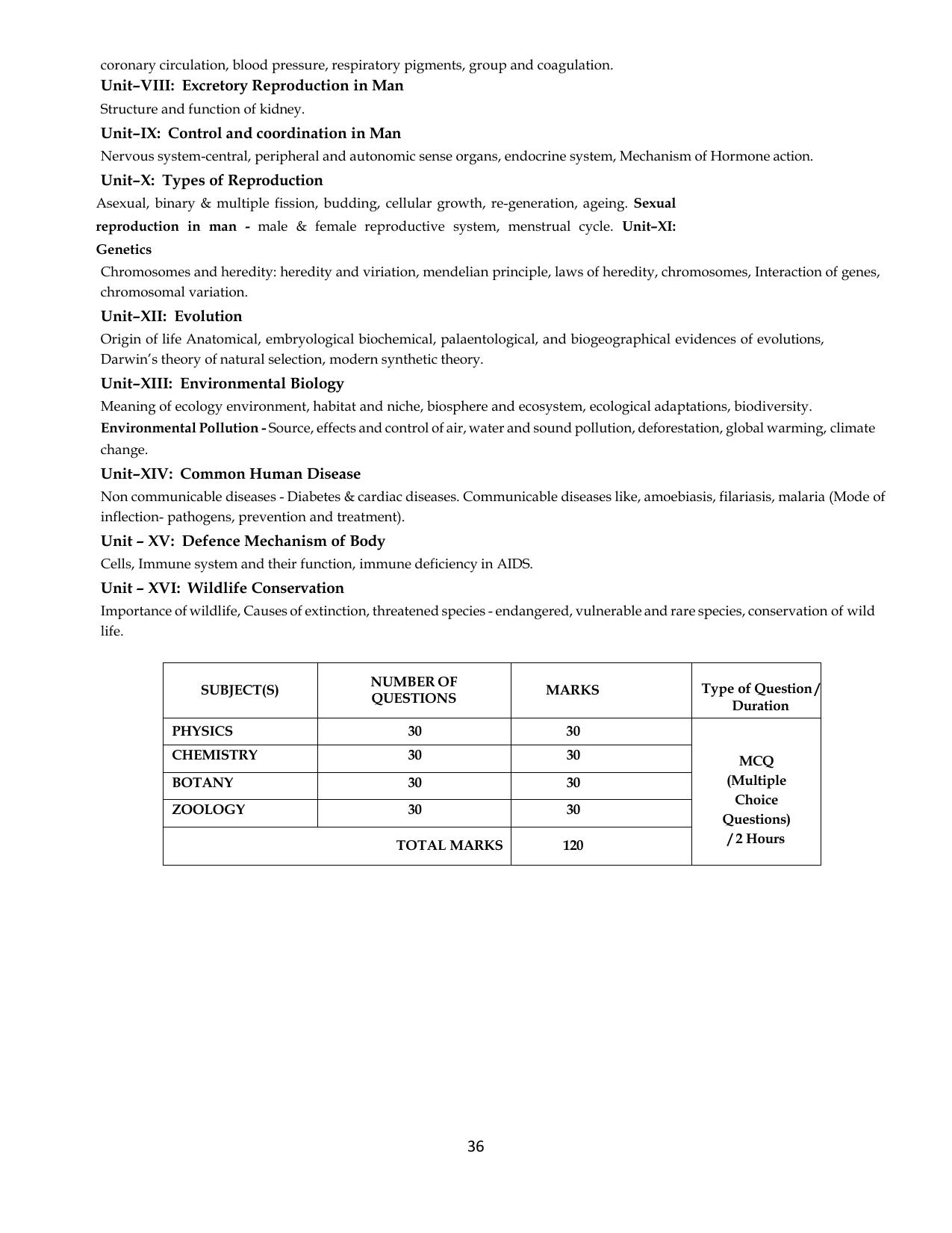

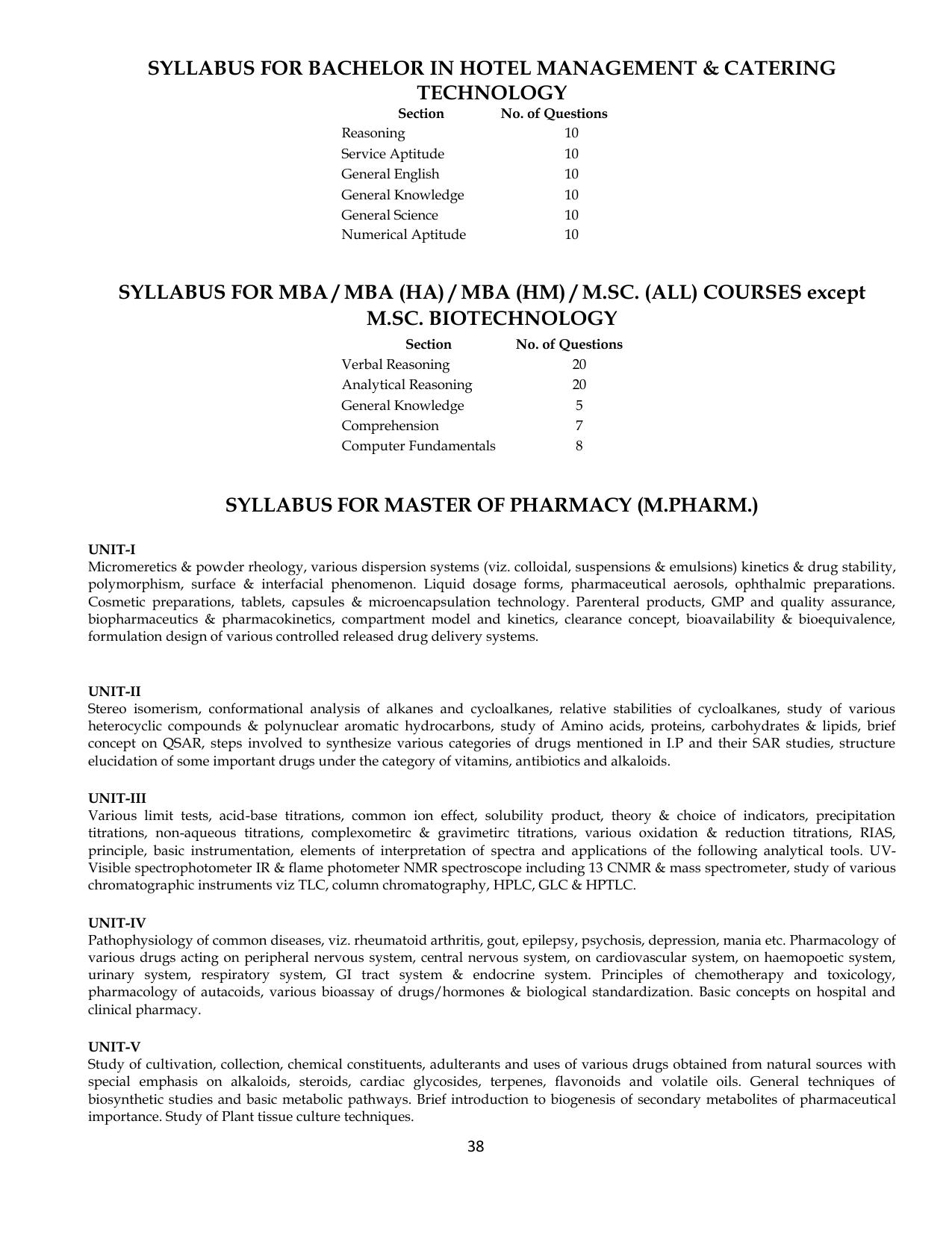



















SAAT Exam Pattern
| Particulars | Details |
|---|---|
| Duration of exam | 2 hours |
| Mode of exam | Online |
| Number of questions | 120 |
| Maximum marks | 120 |
| Marking scheme | Correct answer: +1 Incorrect answer: -1 |
| Sections | Physics Chemistry Mathematics |
How to download SAAT Syllabus?
To download the SAAT 2024 syllabus from indcareer.com, you can easily follow these steps:
Perform a search for “SAAT 2024 syllabus” to land on the relevant page.
On the page, locate and click on the link that provides the syllabus for the SAAT exam, which will open the document.
Once the document is open, find and click on the “Download PDF” link to save the syllabus of Siksha ‘O’ Anusandhan Admission Test to your device.
It is crucial to thoroughly study all the topics mentioned in the syllabus for this common entrance exam. Additionally, solving SAAT previous year question papers will help you understand the types of questions expected in the exam conducted by SOA University, along with the chapter-wise weightage. To enhance your preparation, make sure to cover all the topics in the SAAT syllabus by referring to SAAT 2024 Preparation Books.
SAAT
SAAT is a university-level common entrance exam conducted by Siksha ‘O’ Anusandhan (deemed to be University). The primary objective of this examination is to facilitate admissions to SOA University in various programs such as B.Tech, B.Pharm, B.Sc. Nursing, B.Sc. Agriculture, Lateral Entry to B.Tech, Lateral Entry B.Pharm, Lateral Entry BHMCT, MCA, BHMCT, MBA, MBA (HA), MBA (HM), M.Sc, M.Pharm, M.Tech, M.Sc. Agriculture, M.Sc. Nursing, P.B.B.Sc. Nursing, BA LLB, BBA LLB, LLB, BBA, BCA, LLM, Integrated M.Sc. Biotechnology (IB), and M.Sc. Biotechnology (M.Sc. BioTech.).
Quick Links
SAAT Syllabus – An Overview
The key highlights of this preparation resource are as follows.
| Aspects | Details |
|---|---|
| Name of Exam | SAAT |
| Full Form | Siksha ‘O’ Anusandhan Admission Test |
| Study material Here | Syllabus of SAAT |
| Similar Exams | Common Entrance Exams |
| Official Body for Exam and Its Syllabus | SOA University |
| Full Name of Body | Siksha ‘O’ Anusandhan (deemed to be University) |
| Level of Examination | University Level |
| States of Region Where Institutes Accepting Exam Scores Are | Odisha |
| Exam and Syllabus Official Website | admission.soa.ac.in |
| Courses Where Admission Is Through This Exam | B.Tech, B.Pharm, B.Sc. Nursing, B.Sc. Agriculture, Lateral Entry to B.Tech, Lateral Entry B.Pharm, Lateral Entry BHMCT, MCA, BHMCT, MBA, MBA (HA), MBA (HM), M.Sc, M.Pharm, M.Tech, M.Sc. Agriculture, M.Sc. Nursing, P.B.B.Sc. Nursing, BA LLB, BBA LLB, LLB, BBA, BCA, LLM, Integrated M.Sc. Biotechnology (IB), M.Sc. Biotechnology (M.Sc. BioTech.) |
| Colleges Where Admission Is Through This Exam | SOA University |
